Exploring Air Resistance
Emmette Cox
Product Management Coordinator for Physical Science
March 2016
Air resistance can be a significant factor in many practical applications. The trajectory of projectiles, the velocity of falling objects, and the design of modern vehicles are just a few instances where air resistance affects the movement of an object. However, in most first-year physics classes, air resistance is ignored. One reason is because calculations that involve air resistance can be challenging. Introductory-level physics courses often use situations with ideal conditions to introduce students to the fundamentals of mechanics, and air resistance is included in later courses.
Warm-up activities
Air resistance is an important concept for students to understand, and there are some simple demonstrations and activities that allow students to investigate the effects of drag on moving objects.
One common demonstration of air resistance involves observing a piece of paper and a heavy book as they fall. Hold up both objects and ask students which will fall to the floor faster. Many students will likely select the book. If the book and the paper are held separately and dropped, this will be the case. Repeat the experiment, first placing the paper on top of the book so that the paper is shielded from the air by the book. Then drop the 2 objects together and they should fall at the same rate.
Another standard demonstration in air resistance is the coin and feather. In this demonstration you place a coin and a feather in a long, clear tube. Hold the tube upright and then invert it. The coin falls from 1 end of the tube to the other, while the feather floats slowly down. A valve on 1 end of the tube allows you to remove the air in the tube with a vacuum pump. Once a vacuum is created inside the tube, close the valve and repeat the experiment. This time the coin and the feather fall at the same rate, landing on the bottom end of the tube at the same time.
Historical discoveries
Another warm-up activity for a lesson in air resistance might include a review of some famous experiments involving falling objects. In 1971 David Scott, an astronaut on the Apollo 15 mission, performed an experiment while standing on the moon. A quick Internet search will turn up footage of Commander Scott dropping a hammer and a feather simultaneously on the surface of the moon. This event seems to contradict experience. If someone on the surface of Earth dropped a hammer and a feather from the same height at the same time, the hammer would tend to fall faster, landing sooner on the ground.
A much earlier experiment is said to have happened in the 16th century. Several hundred years before Commander Scott performed his experiment on the moon, Italian physicist and mathematician Galileo Galilei supposedly dropped 2 cannon balls of different masses from the Leaning Tower of Pisa to prove that they would fall at the same rate. It is not clear if that story is true, but it is known that Galileo did perform experiments to show that falling objects, regardless of mass, accelerate toward Earth at the same rate. Galileo’s actual experiments involved rolling spheres with different masses down a long incline in order to slow their motion and allow him to record data for his calculations.
Air resistance
The warm-up activities with the paper and the book, the coin and the feather, and the video of Commander Scott dropping a hammer and a feather on the moon all demonstrate that the difference in the rate of falling objects depends more on the effects of air resistance than on the rate at which gravity accelerates falling objects. Ask students what factors determine the extent to which air resistance affects the movement of a moving object. Factors suggested by students might include shape, mass, speed, or position or orientation of the object. Many students will agree that the force of air resistance on a moving object depends on the speed of the object. The following activity, a study of free-falling coffee filters, allows students to investigate the effects of air resistance on a moving object and how the force is related to the speed of the object.
Coffee filters have a large surface area, and they can be stacked. The rate at which 1 coffee filter falls a given distance can be compared to the rate at which 2 coffee filters fall the same distance, or 3 coffee filters, or 4, etc. As more coffee filters are stacked together, the mass changes, but the shape and the surface area remain the same.
Try dropping a single coffee filter a few times. You will see that the coffee filter falls slowly to the ground. Repeat the process with 2 coffee filters stacked together, then 3 and 4. As more coffee filters are stacked, the rate at which the filters fall increases. For this experiment it is assumed that the coffee filter achieves terminal velocity almost immediately. This means the coffee filter accelerates to a speed where the force of gravity on the coffee filter is equal to the force of air resistance, and the coffee filter falls at a constant rate, its terminal velocity.
If the coffee filter fall at a constant rate, which is its terminal velocity, vT, then the distance the coffee filter travels is expressed by:
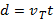
Where:
d = the distance the coffee filter falls
vT = the terminal velocity of the coffee filter
t = the time for the coffee filter to fall the distance, d
How does the air resistance on a moving object vary with speed? If the 2 quantities are directly proportional:
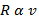
When two quantities are directly proportional, but not necessarily equal, we use the Greek letter alpha, “α”. This statement reads: Air resistance, R, is directly proportional to velocity, v.
The coffee filter reaches terminal velocity very quickly after it is released, so the time the coffee filter spends accelerating from rest to terminal velocity can be ignored, and the coffee filter can be assumed to be traveling at a constant speed for the entire fall. Therefore, if the force of air resistance is directionally proportional to the speed of the coffee filter, then the force of air resistance, R, is proportional to the terminal velocity of the coffee filter:
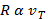
Terminal velocity, vT, is proportional to the weight, W, of the object. This simply means a heavier object will fall faster:
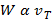
If both the force of air resistance on the falling object, R, and the weight of the object, W, are proportional to the terminal velocity,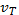 
, then the weight of the object is proportional to the air resistance or drag, R:
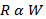
This means that the distance the object travels is proportional to the weight of the object, W, multiplied by the time, t:
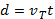
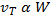
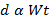
If this is true, then 2 coffee filters will fall twice the distance of a single filter in the same amount of time. This hypothesis can be tested. Hold a single filter at a height of 1 m, and allow the filter to fall from rest to the floor. Record the time of the fall using a stopwatch. Repeat the procedure with 2 coffee filters stacked together, but release the filters from a height of 2 m. Repeat the experiment for 3 coffee filters, dropping the filters from a height of 3 m. If the air resistance is directly proportional to speed, then the amount of time for each trial should be equal. The time for 1 coffee filter to fall 1 m should be the same amount of time as for 2 coffee filters to fall 2 m and for 3 coffee filters to fall 3 m. Students should quickly realize this is not the case.
Another possibility is that the air resistance is proportional to the square of the velocity, v2. If this is true:
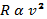
However, since air resistance, R, is proportional to weight, W, the weight is proportional to the square of the velocity:
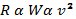
That means v is proportional to the square root of the weight:
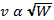
Substituting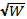 
for v gives an expression for the distance traveled by the filter in a given time:
Activity
Materials
- 6 to 10 Coffee Filters
- Timer or Stopwatch
- Meter Stick or Tape Measure
- Digital Video Recorder (phone, tablet, etc.) (optional)
- Computer (optional)
Safety
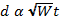
Closely follow the instructions for this activity and abide by established laboratory safety practices, including the use of appropriate personal protective equipment (PPE) such as gloves, goggles, and lab coats or aprons. Do not eat, drink, or chew gum while performing the lab, and wash your hands before and after performing the activity.
Procedure
To observe the velocity of the coffee filter:
- Drop a single coffee filter from a height of 1 m. Observe the motion of the coffee filter, and record the amount of time it takes to reach the ground.
- Stack 2 coffee filters and drop them from a height of 1 m and record the time. Repeat this step several times (always with 2 stacked coffee filters), increasing the height of each drop until the time of the fall is the same as the time recorded in step 1. The time for 1 coffee filter to fall 1 m should be equal to the time for 2 coffee filters to fall from the height found in this step.
- Repeat the process with a stack of 3 coffee filters, 4 coffee filters, and 5 coffee filters. It may be necessary to use a stool or a stairwell to achieve the necessary height for 4 or 5 filters. Take precautions to ensure safety.
- Record the height for each set of filters in Table 1. If possible, verify your measurements by dropping every set of filters simultaneously from the heights found in the experiment. This may require several people, and you may find it useful to record a video so the experiment can be analyzed repeatedly.
Table 1
| Number of Coffee Filters | 1 | 2 | 3 | 4 | 5 |
| Distance to Ground for Simultaneous Landing | 1 m |
Expected results
Students should find that air resistance in this experiment is proportional to the square of the speed. As stated above, this means:
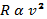
And:
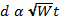
Therefore, the distance required for 2 coffee filters to reach the ground simultaneously will be proportional to the square root of the weight of the 2 coffee filters. If d2 is the distance that 2 coffee filters will fall in the time required for 1 coffee filter to fall 1 m, and W is the weight of 1 coffee filter:
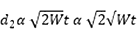
Recall that:
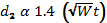
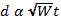
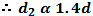
If you drop 1 coffee filter from a height of 1 m, then you should need to drop the set of 2 coffee filters from a height of 1.4 m in order for the 2 coffee filters to reach the ground at the same time as the single coffee filter. If you drop the number of coffee filters specified in Table 2 from the indicated height, you should find that the time it takes each set of coffee filters to reach the ground is the same.
Table 2
| Number of Coffee Filters | 1 | 2 | 3 | 4 | 5 |
| Distance to Ground for Simultaneous Landing | 1 m | 1.4 m | 1.7 m | 2 m | 2.24 m |
Related products
Here are some products to use with this activity.
